SSIM论文简述

1.Introduction

对于图像损失的评估来说，最正确的是人眼的感受（HVS），但是我们对于所有的图片损失用人眼来标记是不现实的（主管方法），因此我们需要一个评估图像损失的函数（客观方法）。

这个函数可以用来在视频流传输时用来估计视频损失来分配带宽、可以用来优化编码器和解码器还可以用来对图像处理的系统进行评分。

这样的损失函数可以根据有original image，只有original image的部分特征，没有original image分为三类，本文提出的SSIM是基于有original image的。

2.Image Quality Assessment Based on Error Sensitivity

对于传统的基于 error sensitivity 的评估函数主要有MSE和基于MSE的PSNR。

MSE = \frac{1}{mn} \sum^{m-1}_{i=0} \sum^{n-1}_{j=0} \left( X(i,j) - Y(i,j) \right)^2

PSNR = 10·\log_{10} \left( \frac{MAX_X ^2}{MSE} \right)

可以看出MSE和PSNR只是对像素点对点分析，忽略了图像整体的结构性，论文中以boat图片为例。

这几张boat图片的MSE是一样的，但是人眼的感觉明显不一样，所以MSE和PSNR是违背HVS的。

论文对此提出了error sensitive有Quality Definition Problem, Suprathreshold Problem, Natural Image Comlexity Problem, Decorrelation Problem, Congnitive Interaction Problem 总结起来主要是两点：1.虽然我们定义了一个误差，但是这个误差对于人眼感受的质量是没有相关性的，2.这个误差函数本身存在问题，包括超阈以及默认了像素间误差的独立分布。

3.Structure Similarity Based Image Quality Assessment

因此作者提出了SSIM，认为HVS对图片信息的感受主要有三部分：光强，对比度，结构信息，而作者认为这三部分是相对独立的。

定义：
\mu_x = \frac{1}{N} \sum^N_{i=1} x_i

\sigma_x = \left( \frac{1}{N-1} \sum^N_{i=1} (x_i - \mu_x)^2 \right)^{1/2}

S(x,y) = f(l(x,y),c(x,y),s(x,y))

考虑满足度量准则（交换律，横小于等于1，只有x=y时等于1）以及人对于刺激的相对变化更敏感而不是刺激的绝对大小，得到等式：
l(x,y) = \frac{2\mu_x\mu_y + C_1}{\mu^2_x + \mu^2_y + C_1}

c(x,y) = \frac{2\sigma_x\sigma_y + C_2}{\sigma^2_x + \sigma^2_y + C_2}

s(x,y) = \frac{2\sigma_{xy} + C_3}{\sigma_x\sigma_y + C_3}

SSIM(x,y) = [l(x,y)]^\alpha[c(x,y)]^\beta[s(x,y)]^\gamma

MSSUN(X,Y) = \frac{1}{M}\sum^M_{j=1} SSIM(x_j, y_j)

为什么SSIM优于PSNR

个人理解人眼对比两张图片其实是在对比两者所含的信息的相对变化。所以我们要找到的一个评估方法分为两部分，提取图片中的信息+比对图片中的信息。

PSNR最大的劣势是在于并没有提取图片中的主要信息，这其实很像给了两个本身维度之间有相关性的矩阵，我们没有对矩阵进行PCA之类的操作，而是直接比对两个矩阵，这样我们其实比对的信息之间是有很强的相关性的。SSIM引入了L，C，S三个函数用于提取图形特征，其实它在这里本质上默认图像遵从高斯分布，它只是提取了高斯分布的\mu，\sigma两个参数，以及用于考虑联合分布的协方差，因此有效的提取了图片中的信息。

在比对图片中的信息环节PSNR也存在一定的问题，人眼敏感的是相对变化，而不是绝对大小，比如一个像素点亮度本来就是200，那它+-5个亮度是没有太大变化的，而一个像素点本身亮度为5，那他+-5个亮度直接变了一个数量级。而SSIM通过分子分母的形式充分考虑了相对变化。

一点猜想

个人猜想SSIM本质上默认两张图像遵从高斯分布，而高斯分布的两个参数\mu和\sigma是相互独立的，因此比对两个图像的差别，只需要比对两个分布的差别也就是两个参数的差别即可。

的确，现实中大部分分布都可以理解为高斯分布，但是如果有些场景下不遵从高斯分布，或者我们不知道数据遵从什么分布的情况下是否有更好的对图片信息提取的方式呢？联想到CNN实质正是对图像结构信息提取的一种方式，我们可不可以训练一个能够很好提取结构信息的神经网络，然后把两张图片分别输入，对比中间每一层提取的信息之间的差别来得到损失函数呢？

之后的Code部分也有尝试对比不遵从高斯分布的图像的SSIM

Code

首先调参使得随机噪点(b图)，增加对比度(c图)，高斯模糊(d图)的MSE=200±0.5

I = imread('boats.bmp');
I_salt = imnoise(I,'salt & pepper', 0.0107);
I_adjust = imadjust(I,[],[], 1.194);
H = fspecial('Gaussian',[11 11],3.55);
I_gauss = imfilter(I,H,'replicate');

[ssimval1, s1] = ssim(I_salt,I);
[ssimval2, s2] = ssim(I_adjust,I);
[ssimval3, s3] = ssim(I_gauss,I);

subplot(2,2,1);imshow(I),title('a');subplot(2,2,2);imshow(I_salt),title('b');
subplot(2,2,3);imshow(I_adjust),title('c');subplot(2,2,4);imshow(I_gauss),title('d');

subplot(1,3,1);imshow(s1),title('b');subplot(1,3,2);imshow(s2),title('c');
subplot(1,3,3);imshow(s3),title('d');

得到噪声处理后的四张图:

得到b,c,d的SSIM为:

	b	c	d
SSIM	0.7513	0.9769	0.7028

SSIM越接近1代表损失越小，人眼观感上确实 loss(c) < loss(b) < loss(d)，说明SSIM确实较好的对这三张图像的损失进行了评估。

图像分布对SSIM的影响

把图像二值化到0和127，噪声处理与之前相同

我们可以看到现在的图像分布明显不是高斯分布了：

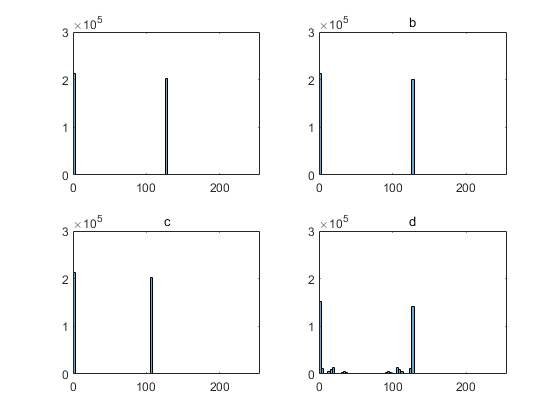
从SSIM值来看依旧和人眼观感基本相同

	b	c	d
SSIM	0.8600	0.9811	0.9260

我们拟合一下高斯分布：

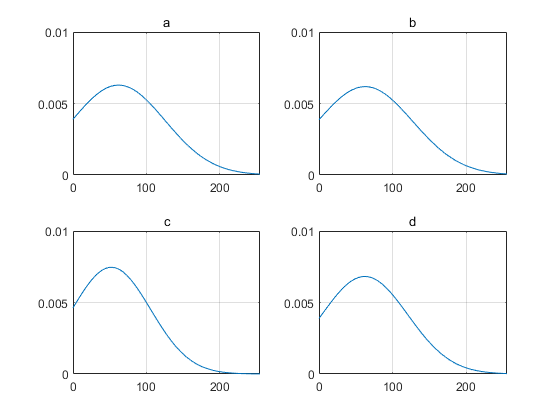
可以发现，即使图像的真实分布远不是高斯分布，我们依旧可以尝试用高斯分布来拟合，图像噪声产生的偏差也会在高斯分布上体现，而且偏差越大，高斯分布的偏差也越大。

所以即使图像分布不遵从高斯分布，在一般的噪声下，对SSIM影响依旧不大。