问题:
九宫图.将1-9九个数字分别填到3*3中,使其每一横\竖\斜都等于15.分别采用深度优先搜索、宽度优先搜索和启发式搜索实现.分析并讨论三种搜索方法的效率,以及启发式函数的设计.
思路:
1-9填充到九宫格本身是个全排列问题,所以先需要对1-9进行全排列,再生成树,最后对树进行搜索,并分析比较搜索算法.
其中由于目标检测函数较为简单,而完整的全排列较为庞大(n!)所以希望能在全排列的同时进行建树并搜索.
全排列&生成树:
传统的全排列方法主要有递归法和字典序法,但是分别存在一些不足,不能边全排列边搜索,所以分析完两种算法之后会采用一种新的交换算法用于在全排列的同时建树和搜索
递归法
简介
(1)n个元素的全排列=(n-1个元素的全排列)+(另一个元素作为前缀);
(2)出口:如果只有一个元素的全排列,则说明已经排完,则输出数组;
(3)不断将每个元素放作第一个元素,然后将这个元素作为前缀,并将其余元素继续全排列,等到出口,出口出去后还需要还原数组;

不足
如图所示,对于递归法,需要生成全部的数字才能进行建树搜索,此时建立的树为完全包含所有结果的树.如果在建立完整的树后再采用搜索算法不如直接在生成树的时候,对每个节点进行检测,这样就失去了建树的意义了,和生成全排列之后直接挨个验证没有什么区别.
字典序法
简介
字典序,就是将元素按照字典的顺序(a-z, 1-9)进行排列。以字典的顺序作为比较的依据,可以比较出两个串的大小。
设P是集合{1,2,……n-1,n}的一个全排列:P=P1P2……Pj-1PjPj+1……Pn(1≤P1,P2,……,Pn≤n-1)
1.从排列的右端开始,找出第一个比右边数字小的数字的序号j,即j=max{i|Pi<Pi+1,i>j}
2.在Pj的右边的数字中,找出所有比Pj大的数字中最小的数字Pk,即k=min{i|Pi>Pj,i>j}
3.交换Pi,Pk
4.再将排列右端的递减部分Pj+1Pj+2……Pn倒转,因为j右端的数字是降序,所以只需要其左边和右边的交换,直到中间,因此可以得到一个新的排列P'=P1P2……Pj-1PkPn……Pj+2Pj+1

不足
如图所示,字典序法生成的全排列是没有分支的树,不适合搜索.
边排列边建树的算法(Powered by Gay傲)
简介
对于集合{a1a2...an}的一个排列a1a2...an,可以把它作为根节点,将a1与之后的元素不断交换生成n-1个子节点,对于每一个子节点,交换第一个元素与之后的元素生成新的子节点.
注:因为会产生重复排列,所以要建立一个hash验证,在生成子节点前去重
证明可行性
(1)首先证明任意两数 i, j的对换可在3步内完成
| 1 | i | j | |
|---|---|---|---|
| 第一步 | i | 1 | j |
| 第二步 | i | j | 1 |
| 第三步 | 1 | j | i |
(2)再通过数学归纳法证明通过有限次交换可生成全排列
①n=2时,a1,a2可以交换生成全排列
②假设n=k-1时成立
当n=k时:
任取ai ,全排列可以分为ai在开头和i不在开头两类:
对于ai在开头的情况,其之后的k-1个元素可以形成全排列,所以ai开头的排列是全排列.
对于ai不在开头的情况,可以把ai在开头的全排列通过有限次交换,形成ai不在开头的全排列
∴n=k时,可以通过有限次交换生成全排列.
搜索
深度优先搜索
简介
深度优先搜索算法是一种用于搜索树的算法。沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
注:为防止深度陷阱,设置搜索深度最大为12层.
流程图
搜索树图

程序
头文件
//
// Created by lizhihao6 on 17-10-5.
//
#ifndef DFS_MAIN_H
#define DFS_MAIN_H
#include <iostream>
#include <vector>
#include <fstream>
using namespace std;
struct node {
int matrix[9] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int layer = 1;
};
void next_matrix();
void back_matrix();
bool isTarget(node putin);
bool isExisted(node putin);
void print_matrix(node putin);
void initHash(node putin);
inline void _swap(int &a, int &b);
void logOut(ofstream &outfile);
vector<node> all;
vector<int> all_hash;
#endif //DFS_MAIN_H
C++程序
#include "main.h"
int main() {
//建立根节点
node begining;
all.push_back(begining);
initHash(begining);
//写入模式打开log文件
ofstream outfile;
outfile.open("DFS.log");
//如果不是目标节点一直循环
while (!isTarget(all.back())) {
logOut(outfile);
//如果到达第十二层开始回溯
if (all.back().layer == 12) {
back_matrix();
} else {
next_matrix();
}
}
logOut(outfile);
print_matrix(all.back());
return 0;
}
//扫描节点下一层
inline void next_matrix() {
bool isNext = false;
node current = all.back();
for (int i = 1; i < 9; i++) {
node newNode;
for (int j = 0; j < 9; j++) {
newNode.matrix[j] = current.matrix[j];
}
_swap(newNode.matrix[0], newNode.matrix[i]);
newNode.layer = current.layer + 1;
//如果子节点不重复,将其加入栈顶
if (!isExisted(newNode)) {
isNext = true;
all.push_back(newNode);
initHash(newNode);
}
}
//如果没有和以前不重复的子节点,则进入回溯函数
if (!isNext) {
back_matrix();
}
}
//回溯函数
inline void back_matrix() {
int layer = all.back().layer;
//因为栈顶元素肯定不是目标节点才会进入回溯函数,所以,删除栈顶
all.pop_back();
//如果删除栈顶之后,新的栈顶比原来栈顶少了一层,说明新的栈顶已无子节点
// (要么新的栈顶应该是和原来栈顶同一层的),所以还要删除新的栈顶,直到新的
//栈顶和原来的栈顶是同一层的.
while ((layer - all.back().layer) == 1) {
layer = all.back().layer;
all.pop_back();
}
}
//检测是否是目标节点
inline bool isTarget(node putin) {
for (int i = 0; i < 3; i++) {
bool row = ((putin.matrix[i * 3] + putin.matrix[i * 3 + 1] + putin.matrix[i * 3 + 2]) == 15);
if (!row) {
return false;
}
}
for (int i = 0; i < 3; i++) {
bool colum = ((putin.matrix[i] + putin.matrix[i + 3] + putin.matrix[i + 6]) == 15);
if (!colum) {
return false;
}
}
bool oblique = (((putin.matrix[0] + putin.matrix[4] + putin.matrix[8]) == 15) &&
((putin.matrix[2] + putin.matrix[4] + putin.matrix[6]) == 15));
if (!oblique) {
return false;
}
return true;
}
//检测节点是否重复
inline bool isExisted(node putin) {
int hash = 0;
for (int i = 0; i < 8; i++) {
hash = hash << 4;
hash = hash + putin.matrix[i];
}
for (int i = 0; i < all_hash.size(); i++) {
if (hash == all_hash[i]) {
return true;
}
}
return false;
}
//打印节点
inline void print_matrix(node putin) {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cout << putin.matrix[i * 3 + j] << " ";
}
cout << endl;
}
cout << endl;
}
//一个9位的排序,只要知道前8位就知道了整个排序,1-9最多用3位二进制表示,所以总共用32位,一个int储存变量hash值
inline void initHash(node putin) {
int hash = 0;
for (int i = 0; i < 8; i++) {
hash = hash << 4;
hash = hash + putin.matrix[i];
}
all_hash.push_back(hash);
}
//将每次栈顶存入log
inline void logOut(ofstream &outfile) {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
outfile << all.back().matrix[i * 3 + j] << " ";
}
outfile << endl;
}
outfile << endl;
}
inline void _swap(int &a, int &b) {
int c = a;
a = b;
b = c;
}广度优先搜索
简介
广度优先要求按层级搜索树,先把树的一层搜索完毕,再搜索下一层,直到找到目标节点为止.具体实现可以通过建立一个队列,先通过队列头生成子节点,再把子节点放入队列尾,最后再删除队列头,不断循环,这样可以保证后生成的子节点,即靠后的层级会晚一些进行搜索.
流程图

搜索树图
按照字母序进行搜索
程序
头文件
//
// Created by lizhihao6 on 17-10-5.
//
#ifndef BFS_MAIN_H
#define BFS_MAIN_H
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <fstream>
using namespace std;
struct node {
int matrix[9] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
// int layer = 1;
};
void next_matrix();
bool isTarget(node putin);
bool isExisted(node putin);
void print_matrix(node putin);
void initHash(node putin);
inline void _swap(int &a, int &b);
void logOut(ofstream &outfile);
using namespace std;
queue<node> all;
vector<int> all_hash;
#endif //BFS_MAIN_H
C++程序
#include "main.h"
int main() {
//写入模式打开log文件
ofstream outfile;
outfile.open("BFS.log");
logOut(outfile);
//初始化初始节点
node begining;
all.push(begining);
initHash(begining);
//如果队列最前面不是目标节点就一直循环
while (!isTarget(all.front())) {
logOut(outfile);
next_matrix();
all.pop();
}
print_matrix(all.front());
return 0;
}
//生成下一层节点,并放在队列尾
inline void next_matrix() {
for (int i = 1; i < 9; i++) {
node newNode;
memcpy(newNode.matrix, all.front().matrix, 9 * sizeof(int));
_swap(newNode.matrix[0], newNode.matrix[i]);
//如果以前没有重复,就放入队列尾
if (!isExisted(newNode)) {
all.push(newNode);
initHash(newNode);
}
}
}
//验证是否为目标节点
inline bool isTarget(node putin) {
for (int i = 0; i < 3; i++) {
bool row = ((putin.matrix[i * 3] + putin.matrix[i * 3 + 1] + putin.matrix[i * 3 + 2]) == 15);
if (!row) {
return false;
}
}
for (int i = 0; i < 3; i++) {
bool colum = ((putin.matrix[i] + putin.matrix[i + 3] + putin.matrix[i + 6]) == 15);
if (!colum) {
return false;
}
}
bool oblique = (((putin.matrix[0] + putin.matrix[4] + putin.matrix[8]) == 15) &&
((putin.matrix[2] + putin.matrix[4] + putin.matrix[6]) == 15));
if (!oblique) {
return false;
}
return true;
}
//验证是否和已生成节点重复
inline bool isExisted(node putin) {
int hash = 0;
for (int i = 0; i < 8; i++) {
hash = hash << 4;
hash = hash + putin.matrix[i];
}
for (int i = 0; i < all_hash.size(); i++) {
if (hash == all_hash[i]) {
return true;
}
}
return false;
}
//打印节点
inline void print_matrix(node putin) {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cout << putin.matrix[i * 3 + j] << " ";
}
cout << endl;
}
cout << endl;
}
//1-9的全排列,只需要知道前8位排列方式就知道整个排列方式
//1-9最大需要三个bite存储,8位需要32bite也就是一个int存储
inline void initHash(node putin) {
int hash = 0;
for (int i = 0; i < 8; i++) {
hash = hash << 4;
hash = hash + putin.matrix[i];
}
all_hash.push_back(hash);
}
inline void _swap(int &a, int &b) {
int c = a;
a = b;
b = c;
}
//输出队列头到日志
inline void logOut(ofstream &outfile) {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
outfile << all.front().matrix[i * 3 + j] << " ";
}
outfile << endl;
}
outfile << endl;
}启发式搜索
简介
启发式搜索结合了深度优先和宽度优先,它对每一次生成的节点通过一个估值函数h(n)进行估值,其中估值越小代表越接近目标节点,因此每次会选择估值最小的节点作为下次生成子节点的母节点.
启发式函数设计
设置所有节点的初始value为8,如果节点的横竖斜任意一个满足相加=15,则value-1,表示更接近目标节点.
流程图
搜索树图
程序
头文件
//
// Created by lizhihao6 on 17-10-4.
//
#include <iostream>
#include <vector>
#include <fstream>
#include <cstring>
using namespace std;
#ifndef A_MAIN_H
#define A_MAIN_H
struct node {
int matrix[9] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int value = 8;
};
void next_matrix();
bool isExisted(const node &putin);
void print_matrix(const node &putin);
void initHash(const node &putin);
int value(const node &putin);
inline void _swap(int &a, int &b);
void insert_matrix(node &putin);
void logOut(ofstream &outfile);
vector<node> all;
vector<int> all_hash;
#endif //A_MAIN_H
C++程序
#include "main.h"
int main() {
//初始化根节点
node begining;
begining.value = value(begining);
all.push_back(begining);
initHash(begining);
//写入模式打开log文件
ofstream outfile;
outfile.open("A.log");
logOut(outfile);
int time =0;
//如果没搜索到目标建立子节点
while (all.back().value != 0) {
next_matrix();
logOut(outfile);
}
//搜索到后打印目标节点
print_matrix(all.back());
outfile.close();
return 0;
}
//打印每次value最低(最接近目标)的节点
inline void logOut(ofstream &outfile) {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
outfile << all.back().matrix[i * 3 + j] << " ";
}
outfile << endl;
}
outfile << endl;
}
//产生新子节点
inline void next_matrix() {
//将value最低(最接近目标)的节点暂存(用来产生子节点)之后删除(已验证不为目标节点)
node current = all.back();
all.pop_back();
for (int i = 1; i < 9; i++) {
node newNode;
memcpy(newNode.matrix, current.matrix, 9 * sizeof(int));
_swap(newNode.matrix[0], newNode.matrix[i]);
//验证新产生的子节点是否已经存在,不存在的话判断value,之后进入差入函数
if (!isExisted(newNode)) {
newNode.value = value(newNode);
print_matrix(newNode);
cout<<newNode.value<<endl;
insert_matrix(newNode);
initHash(newNode);
}
}
}
inline void _swap(int &a, int &b) {
int c = a;
a = b;
b = c;
}
//验证是否已经存在
inline bool isExisted(const node &putin) {
int hash = 0;
for (int i = 0; i < 8; i++) {
hash = hash << 4;
hash = hash + putin.matrix[i];
}
for (int i = 0; i < all_hash.size(); i++) {
if (hash == all_hash[i]) {
return true;
}
}
return false;
}
inline void print_matrix(const node &putin) {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cout << putin.matrix[i * 3 + j] << " ";
}
cout << endl;
}
cout << endl;
}
//一个9位的排序,只要知道前8位就知道了整个排序,
//1-9最多用3位二进制表示,所以总共用32位,一个int储存变量hash值
inline void initHash(const node &putin) {
int hash = 0;
for (int i = 0; i < 8; i++) {
hash = hash << 4;
hash = hash + putin.matrix[i];
}
all_hash.push_back(hash);
}
//估值函数,设定只要横/竖/斜有一个等于15,value就--
inline int value(const node &putin) {
int value = 8;
for (int i = 0; i < 3; i++) {
bool row = ((putin.matrix[i * 3]
+ putin.matrix[i * 3 + 1] + putin.matrix[i * 3 + 2]) == 15);
if (row) {
value--;
}
}
for (int i = 0; i < 3; i++) {
bool colum = ((putin.matrix[i]
+ putin.matrix[i + 3] + putin.matrix[i + 6]) == 15);
if (colum) {
value--;
}
}
bool oblique1 = ((putin.matrix[0] + putin.matrix[4] + putin.matrix[8]) == 15);
bool oblique2 = ((putin.matrix[2] + putin.matrix[4] + putin.matrix[6]) == 15);
if (oblique1) {
value--;
}
if (oblique2) {
value--;
}
return value;
}
//将新节点按照value从大到小插入vector
inline void insert_matrix(node &putin) {
if (all.size() == 0) {
all.push_back(putin);
return;
} else {
for (int i = 0; i < all.size(); ++i) {
if (putin.value > all[i].value) {
all.insert(all.begin() + i, putin);
return;
}
}
all.push_back(putin);
return;
}
}不同搜索算法的比较
时间复杂度
由于不同搜索方式生成子节点,验证子节点是否重复的方式均一致,所以都按照O(1)计算.
深度优先
深度优先每次生成子节点都放入栈顶,每次延伸都需要经过一支分叉,所以所需总步骤为:C1全部节点数+C2全部分支数.即O(C1n!+C2(n!-1))=O(n!).
广度优先
广度优先每次取用节点从队列头取出,生成子节点都放入队尾,每次延伸都需要经过一支分叉,所以所需总步骤也为:C1全部节点数+C2全部分支数.即O(C1n!+C2(n!-1))=O(n!).
启发式搜索
启发式搜索除了要经历所有节点和所有分支以外,每次还需要将新生成的节点插入排序到包含已生成的所有子节点的链表中,所以需要的总步骤为:C1全部子节点+C2全部分支数+(1+2+3+...+全部子节点数),即O(C1n!+C2(n!-1)+(n!)2)=O[(n!)2].
总结
从最坏时间复杂度上看,深度优先和广度优先的复杂度一致,启发式搜索由于每次需要将新生成的子节点进行插入排序,所以最坏时间复杂度最高,但是实际搜索效率并非如此.
实际搜索效率测试
测试方法
随机生成不同的根节点作为测试集.用每种搜索算法对测试集的每个根节点进行搜索,取每种搜索的平均搜索时间进行对比.
数据集
将1-9随机排列,生成10组不同的根节点
{8, 4, 2, 3, 1, 6, 7, 5, 9},
{7, 5, 4, 9, 6, 2, 8, 1, 3},
{9, 3, 1, 5, 2, 4, 6, 8, 7},
{7, 1, 4, 8, 5, 6, 3, 2, 9},
{2, 7, 4, 9, 8, 5, 6, 3, 1},
{5, 6, 3, 7, 2, 9, 1, 4, 8},
{1, 9, 2, 7, 4, 8, 5, 6, 3},
{3, 8, 9, 7, 5, 6, 4, 1, 2},
{9, 3, 1, 7, 8, 2, 6, 5, 4},
{9, 8, 1, 2, 3, 7, 6, 5, 4}
测试结果
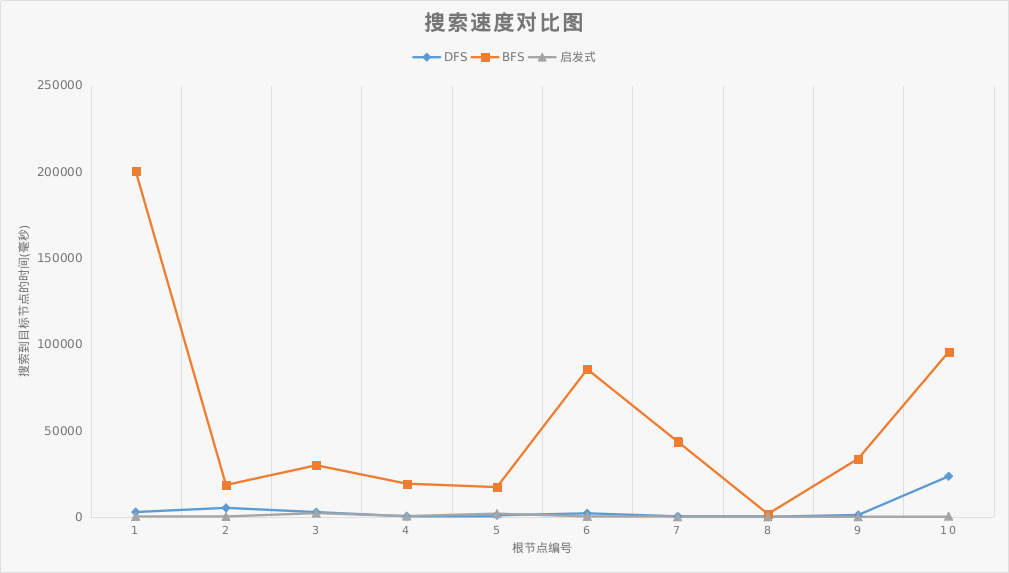
| 搜索方式 | DFS | BFS | 启发式 |
|---|---|---|---|
| 测试集平均搜索时间(ms) | 3848.2391 | 54464.8969 | 526.3955 |
从图中我们可以看出在本搜索中DFS和启发式搜索远优于BFS,而从平均搜索时间来看,启发式搜索的搜索效率也高于DFS数倍.
不同启发式函数的比较
g(n)对搜索效率的影响
A*搜索的估值函数其实包含两部分f(n)=g(n)+h(n)
其中g(n)为当前节点到根节点的距离,h(n)为当前节点到目标节点的估计值
之前在和DFS,BFS横向对比时,启发式函数没有包含g(n)部分,也就是完全变成了BestFirst搜索,现来探究一下g(n)对启发式函数搜索效率的影响
g(n)的作用
1.当h(n)估值若干个节点价值相同时,会选择早先产生的节点作为下一步的节点,但是当搜索深度已经很深的时候,我们即使找到目标节点也不能保证是通过最短路径找到,而g(n)的引入在一定程度上会加快效率.
2.但是加入g(n)后,比如执行到第7层,有一个子节点的h(n)估值很接近于0,也就是很接近目标节点,但是在引入g(n)后,它的估值甚至还不如第一层的一些h(n)估值很高的节点.
个人认为,g(n)的引入主要想减少DFS的影响,加大BFS的部分,对于实际效率猜想不同情境下会差别较大.
g(n)引入后测试
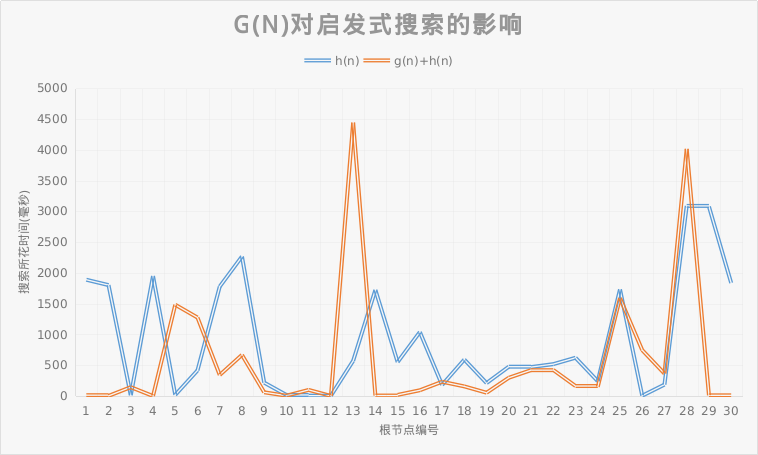
| 搜索方式 | h(n) | g(n)+h(n) |
|---|---|---|
| 测试集平均搜索时间(ms) | 916.4648333 | 576.1146667 |
从图中可以看出,大部分情况下g(n)的引入会使效率提高,从统计上看,总效率会比不引入g(n)提高一倍左右.
启发式函数的设计
几种不同的启发式函数
1.h1(n)=横竖斜 != 15的数量
2.h2(n)=max [横竖斜 != 15的数量,数组中间等于5? 0 : 8]
(考虑到最终解矩阵中间必须为5,所以给中间为5一个较大的比重)
3.h3(n)=横竖斜 != 15的数量+(横竖斜 != 15的数量)%2
(考虑到一部分不满足15的数量为奇数的情况下,需要交换的次数与比其大1的偶数相同,所以将奇数的value增加1)
4.h4(n)=横竖斜 != 15的数量+rand(0,0.9)
(因为之前再选取等value的时候完全是依靠建立节点的先后顺序,因此引入随机性来加强下一个节点的随机性)
效率对比测试
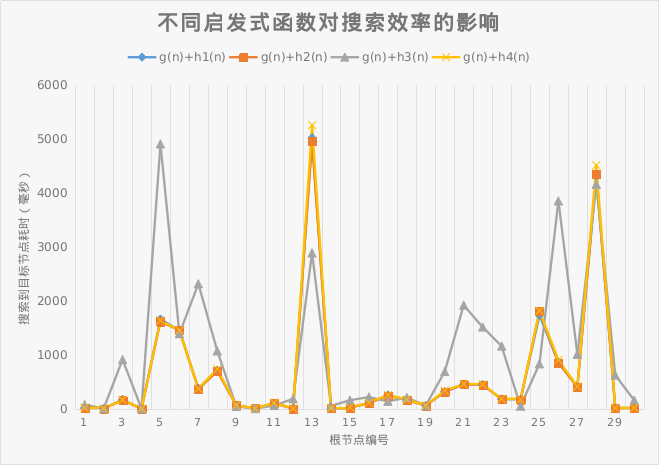
| 搜索方式 | g(n)+h1(n) | g(n)+h2(n) | g(n)+h3(n) | g(n)+h4(n) |
|---|---|---|---|---|
| 测试集平均搜索时间(ms) | 634.6796333 | 632.8587 | 1019.7293 | 656.1575333 |
从此我们可以看出,只有h(3)n对搜索效率负面影响很大,其余的启发式函数搜索效率几乎无差别.
总结
都写完了也没法评判这个时间花的值不值了,借这次机会学会了算复杂度,画flowchat...不说了,补EE专业课和线代去了.








Comments | NOTHING